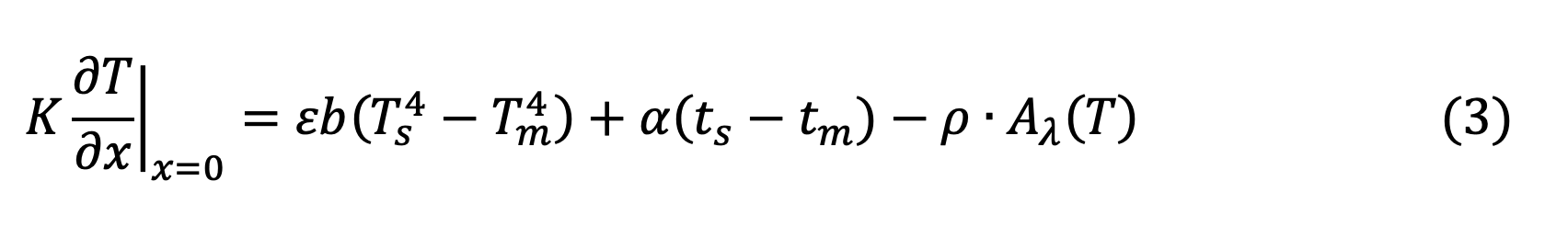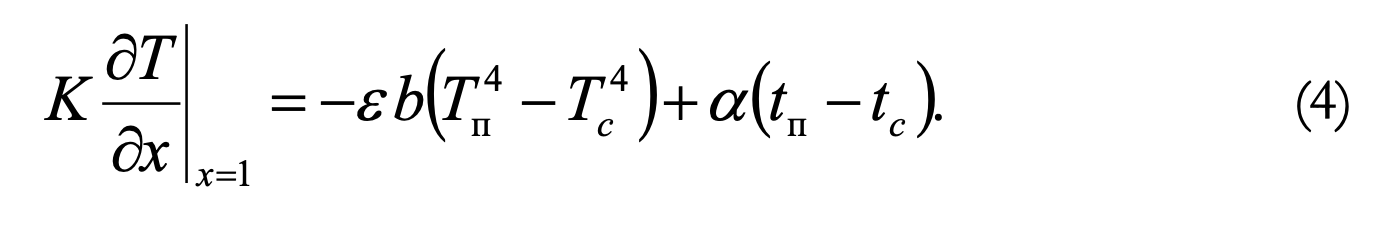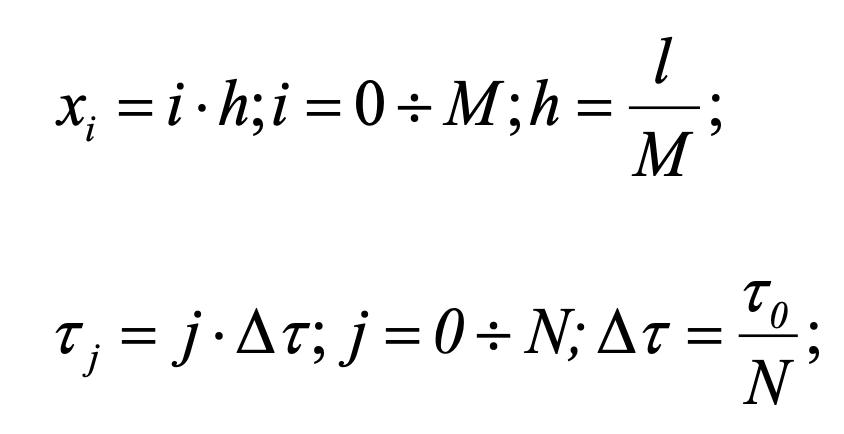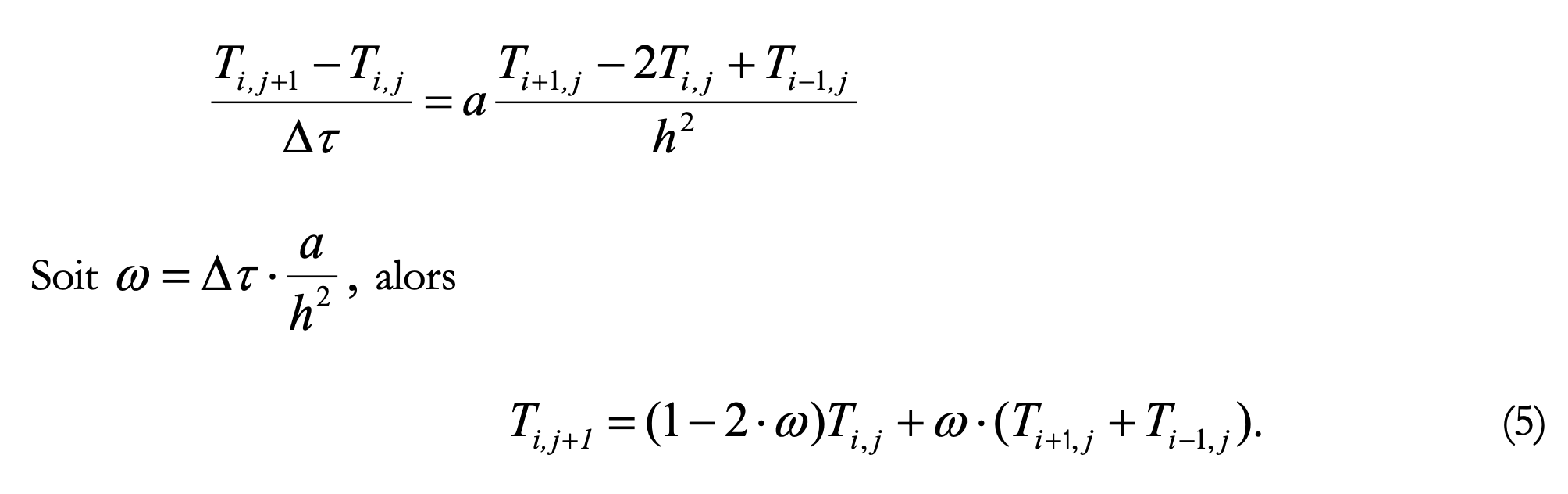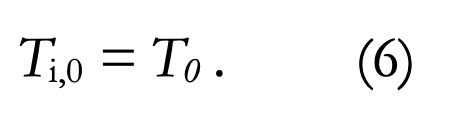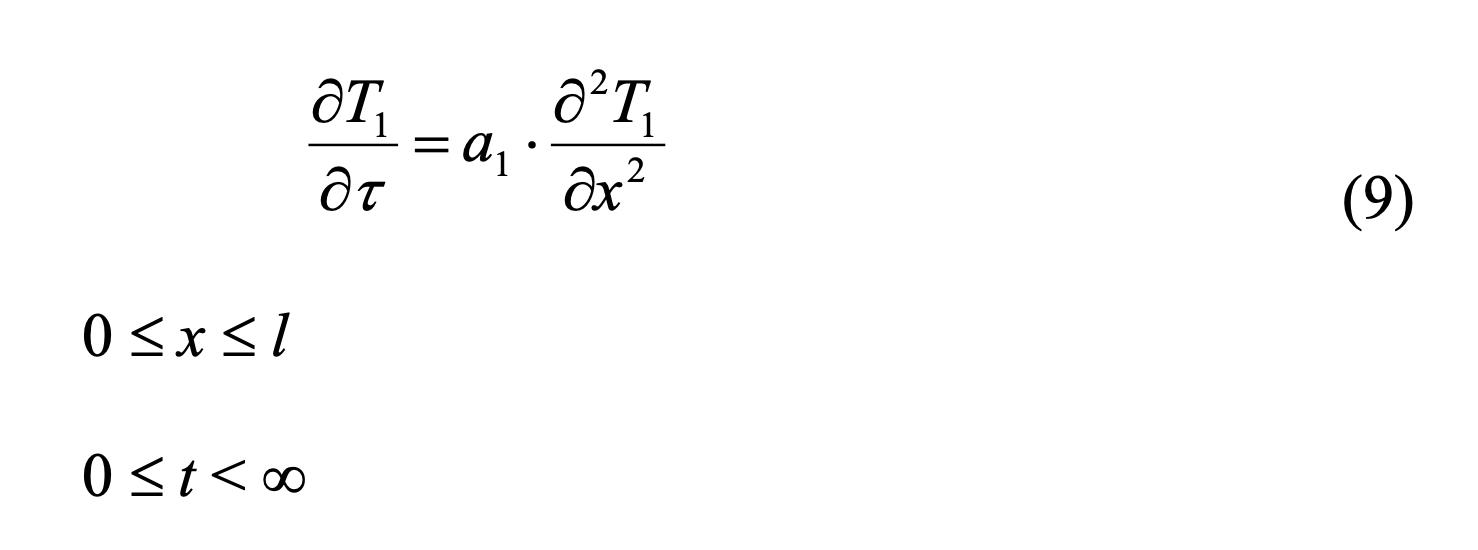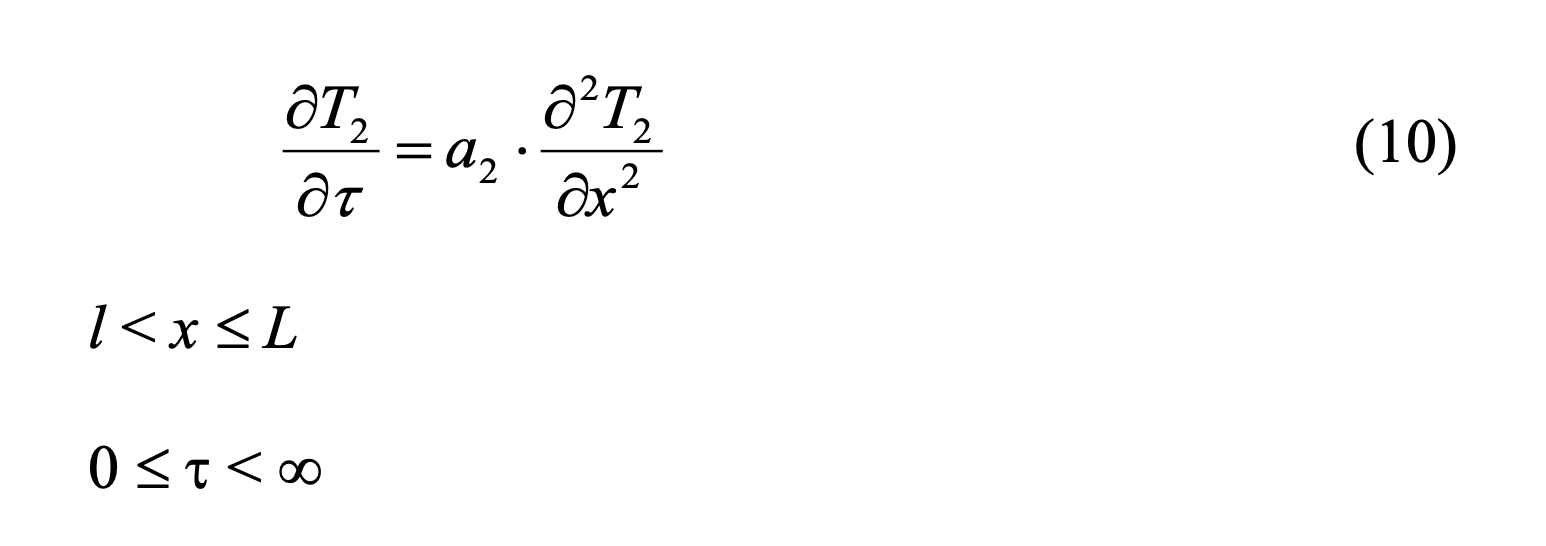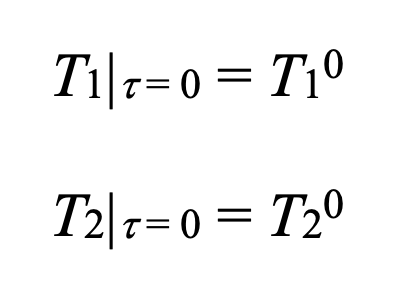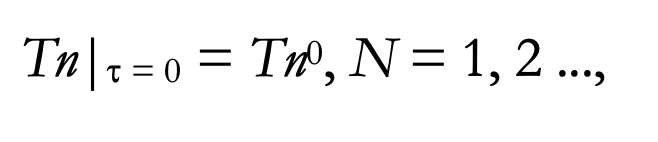Grigori Petrovitch Grabovoï
G. P. Grabovoï donnera une série de conférences sur le thème de la prévision et du contrôle des événements à destination des étudiants du département du système de qualité orienté vers la prévision (SQOP). Il assurera la formation et la certification des étudiants dans la capacité d'utiliser des informations à visée prévisionnelle pour contrôler des processus technologiques et économiques.
École supérieure du « Centre des sciences. »
Recherche et analyse des définitions fondamentales des systèmes optiques destinés à la prévention de catastrophes et au contrôle axé sur la prédiction des microprocessus
RECHERCHE ET ANALYSE DES DÉFINITIONS FONDAMENTALES DES SYSTÈMES OPTIQUES DESTINÉS À LA PRÉVENTION DE CATASTROPHES ET AU CONTRÔLE AXÉ SUR LA PRÉDICTION DES MICROPROCESSUS
Ce
travail a été réalisé en utilisant la méthode de l’auteur, consistant à
procéder à une analyse numérique de la forme informationnelle.
Pertinence
Dans
l’objectif de prédire et de prévenir les catastrophes, une théorie physique et
mathématique ainsi qu’un dispositif ont été conçus, permettant de déterminer la
composante informationnelle relative aux événements futurs. Étant donné que de
nombreux accidents d’origine naturelle ou technologique se produisent sans base
statistique définie, cette découverte permettant d’obtenir des informations
précises sur le futur est particulièrement pertinente, car elle comprend les
moyens d’éviter ces catastrophes.
Les
principes des technologies théorique et instrumentale à l’œuvre sont basés sur
le postulat d’une interconnexion de tous les éléments de la réalité [1]. On y
définit une approche structurelle et analytique visant à élaborer des systèmes
de contrôle, dans lesquels chaque élément concourt au développement harmonieux
de tous les autres éléments de la réalité. Ce travail montre comment créer une
substance matérielle, en utilisant un mécanisme de contrôle du champ des
événements futurs. Selon cette technologie, on peut, à partir du présent,
introduire des impulsions de contrôle dans des cristaux, de manière à obtenir
la substance voulue dans un certain point de l'espace et du temps futurs.
Objets
d’étude :
Séismes,
unités de production, toute réalité dont les paramètres sont connus ou inconnus.
Nouveautés
scientifiques de cette étude :
-
C’est la première
fois qu’une méthode permettant d’obtenir des informations sur les événements
futurs est mise en œuvre de manière théorique et pratique ;
-
C’est la première
fois qu’est proposée une démarche permettant de contrôler tout objet
informationnel à partir de l’endroit de ses propriétés informatives actuelles ;
-
Elle permet de
contrôler avec précision des objets de la réalité dont les caractéristiques
sont inconnues ou ne peuvent être déterminées à temps.
Valeur
théorique de ce travail :
- Au niveau des définitions fondamentales des systèmes
optiques ;
- Au niveau des généralisations et des implications de ces
définitions ;
- Dans l’élaboration de technologies structurelles et
analytiques de prévention et de prévision des catastrophes, qui présentent notamment
une menace pour le monde.
Implications pratiques de cette recherche :
- Création d’un dispositif de prévention et de prévision
des tremblements de terre et des catastrophes industrielles, grâce à des
méthodes de modélisation informatique consistant à numériser la forme de
l’objet, création d’une orientation nouvelle dans le contrôle des
microprocessus ;
- Élargissement des résultats obtenus à l’ensemble des
objets informationnels ;
- Obtention de principes méthodologiques permettant de
créer des systèmes technologiques harmonisés dans tous les milieux.
Évaluation et mise en œuvre des résultats
Les résultats ont été évalués et mis en œuvre en
utilisant la technologie de l’auteur, qui consiste à analyser numériquement la
forme de l’information attribuée à tout objet informationnel, sur le principe
de l’interconnexion de tous les éléments informationnels [2]. En se basant sur
une expérience personnelle du contrôle de précision par le biais de méthodes
irrationnelles, et des principes pour transposer les résultats de ce contrôle sur
des structures matérielles (ces résultats sont décrits dans la thèse de
doctorat « Structures appliquées du champ créateur de
l’information »), des données numériques incluant des résultats théoriques
et pratiques ont été obtenues, qui prouvent l’exactitude de ce mécanisme de
travail structurel et analytique. Les données sur la surveillance de la surface
terrestre par les systèmes de contrôle des satellites planétaires, fournies par
l'Agence de Surveillance et de Prévision du Ministère des Situations d'urgence
de Russie ont été utilisées comme matériel initial pour vérifier la conformité
de l’analyse numérique produite par le dispositif par rapport aux processus réels.
1. Introduction
Une étude des processus de la réalité basée sur le fait
que les événements futurs peuvent être connus dans le présent permet de prévenir
les catastrophes et de contrôler les événements futurs. L’essence de cette
démarche est de considérer les événements futurs comme des structures qu’il est
possible de contrôler depuis le présent [3]. L’information des événements
futurs se manifeste dans le champ où le futur se transforme en présent. Ce
champ de transition est doté de sept coordonnées : trois coordonnées
indiquant l’espace du temps présent, la coordonnée temporelle, deux coordonnées
d’intervalles temporels correspondant au passé et au futur, et la coordonnée correspondant
à la réaction de l’objet. C’est, en général, dans cette dernière qu’on trouve
le champ d’interaction de tous les objets informationnels, et de la perception
humaine en particulier. Pour sauver un objet informationnel de la destruction,
on peut transformer l’intervalle du futur grâce à l’intervalle du passé, en
projetant ses données dans l’espace tridimensionnel du temps présent. Ces
signaux peuvent être enregistrés comme des systèmes optiques. Lorsque la
lumière traverse le milieu optique d’un cristal, elle se diffuse en composants
correspondant à tous les champs informationnels. Le composant lumineux qui
s’organise comme une réflexion des événements futurs à travers l’intervalle
passé, se présente sous forme de point, éloigné à l’infini du cristal, mais situé à l’intérieur de lui au niveau physique, ce qui permet
d’enregistrer et de décoder un événement futur comme on décrit les propriétés
d’un système optique. Si l’on détient dans le présent un fragment des processus
futurs, on peut alors créer avec exactitude une matière du futur correspondant
à une phase de développement harmonieux. En sachant comment les signaux issus
du futur se distribuent dans le champ de contrôle de la réalité, il est
possible de prévenir les événements catastrophiques en créant un système
optique harmonisant tous les domaines d'information. Les signaux lumineux sont
traités avec précision car la lumière a la propriété de se diviser dans les
cristaux en composantes du temps présent et futur. Il est possible d’observer
le sens physique de ce phénomène par modélisation en considérant les propriétés
de la lumière dans un intervalle de temps inférieur à 10-17 secondes.
On peut alors voir le segment informationnel correspondant au temps futur pour
un intervalle temporel supérieur à 10-12 secondes entrer en contact
avec le segment informationnel correspondant au temps présent. L’endroit où le
segment du futur et celui du temps présent entrent en contact peut être décrit,
au niveau physique, par un système cristallin. C’est ce système qui permet à la
lumière de se diffuser sur les éléments du présent et du futur. Ainsi, en fixant
les paramètres du système optique sur la base des lois de la structure
cristalline, il est possible de contrôler la matière et de créer les éléments
événementiels de la manière voulue.
2. Définitions
fondamentales
des systèmes optiques
Les définitions fondamentales des systèmes optiques sont
déterminées selon trois champs.
2.1. Le premier champ
est celui de la définition de l’interaction informationnelle entre les objets
dans le futur, en tant qu’espace de départ pour percevoir le temps présent.
2.1.1. Formule et données de découverte de l’énergie du
futur :
(1)
L’énergie du futur
a été définie : elle se
compose de l’énergie du passé multipliée par l’espace de distribution de
l’énergie du présent et divisée par l’espace de distribution de l’énergie du
passé

où Ψ : énergie du futur, E : énergie du passé, W : espace de distribution de l’énergie
du présent, U : espace de distribution de l’énergie du passé.
Cette définition de l’énergie du futur
est innovante car elle
met en lumière un segment énergétique propre aux objets informationnels futurs,
qui permet de déterminer le futur à partir de valeurs préalablement définies.
Le champ d’application de cette définition concerne tous les
systèmes de contrôle et de transformation optique de l’information. Dans les
systèmes optiques à base de cristaux, on observe une diffusion de la lumière correspondant
à la découverte de l’énergie du futur.
Ψ peut être déduit en définissant W
comme l’espace des cristaux, U comme celui du champ mesuré, et E
comme l’énergie issue de l’impulsion lumineuse. Sur la base de la
classification de Ψ relative à la norme des événements, un contrôle
prévisionnel est établi.
2.2. Le second champ est celui de la définition de l’énergie du passé.
2.2.1. Formule et données de définition de l’énergie du passé :
L'énergie
du passé est définie comme le produit de
l'énergie actuelle (énergie du présent) et des fonctions d'intersection des
énergies du futur et du passé.

où Ep : énergie du présent, F : fonction
d'intersection des énergies du futur et du passé.
Cette définition de l’énergie du passé est innovante car des phénomènes de la réalité autrefois inconnus ont été
découverts, qui permettent de définir l’énergie correspondant à plusieurs
temporalités dans un champ unique.
Le champ d’application de cette définition de l’énergie du
passé concerne les systèmes de reconnaissance des signaux provenant d’objets
situés dans n’importe quelle réalité, même si la structure de cette réalité est
inconnue. Au niveau conceptuel, pour des valeurs infinies, F sera identique
à Ψ. Dans la structure des systèmes optiques cristallins, la
reconnaissance du signal s’effectue en fixant F dans les zones où le signal
interagit avec les cristaux.
2.3. Le
troisième domaine est celui de la définition de la réalité générale.
2.3.1. Formule
et données de définition de la réalité générale :
On définit une réalité commune à tous
les processus de la réalité :
l’impulsion de tout événement se transforme dans le temps actuel (dans les
événements du présent) au niveau de la zone de recoupement du futur et du
passé. La réalité de tout processus se transforme en un champ au contenu
éloigné et unique dans un environnement reproductible, c’est-à-dire que tout
processus est tant unique qu’il peut se répéter dans le champ où l’énergie se
transforme en présent (en un événement du temps présent). En conséquence, dans
la phase de transformation, tout élément de la réalité est indestructible et
reproductible, quelles que soient les conditions du milieu interne et externe. Tout
élément de la réalité peut donc être restauré.
La solution pour prévenir une catastrophe se trouve donc au sein même de
l’impulsion de l’événement futur. Cette découverte peut être formulée
ainsi :
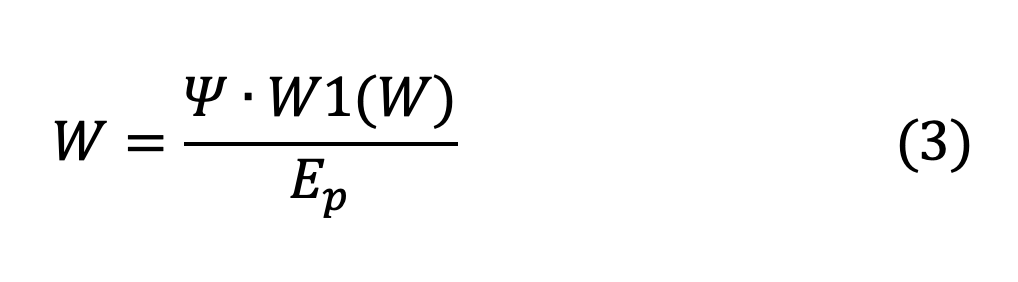
où W : réalité générale, W1 :
fonction de la réalité générale des phénomènes à fixer.
Cette définition de la réalité générale est innovante car elle définit pour la première fois un environnement
fonctionnel permettant de transformer et de décrire tout processus de la
réalité à partir d’un seul point.
Le champ d’application
de cette définition de la réalité générale dans les systèmes optiques
conducteurs permet d’identifier une impulsion transformant n’importe quel
milieu, afin de contrôler la réalité. Plus généralement, cette découverte
permet de déterminer tous les phénomènes de la réalité.
Selon
ces définitions fondamentales des systèmes optiques, les lois de contrôle de
l’impulsion optique peuvent être mises en pratique.
Selon la première loi, les
systèmes optiques à base de cristaux reproduisent le reflet d'événements futurs,
ayant traversés d’une picoseconde l’intervalle du passé.
La seconde
loi est celle
du mouvement du signal optique, orienté à la fois vers les systèmes de fixation
et vers un environnement aux propriétés indéfinies. Dans ce contexte, il est
possible de distinguer la constante informationnelle déterminant le contrôle des
environnements à structure indéterminée.
Selon
la troisième loi, en
reconnaissant le champ de projection du futur sur le présent, sur la base d’une
impulsion variée selon les différents milieux, la structure d’un dispositif
harmonisant tous les systèmes peut être établie.
Selon
la quatrième loi, le
système défini par un signal optique est toujours défini pour des processus
infinis. Il découle de cette quatrième loi que tous les processus de la réalité
peuvent être décrit dans chacun de ses champs (c’est pourquoi l’univers réagit
à des changements qui n’ont déjà plus cours). Seule l’éternité existe, et elle
se contient elle-même. On en déduit aussi que l’éternité du cristal est le
reflet de la réalité établie.
En
synthétisant les définitions fondamentales des systèmes optiques, on parvient à
déterminer un mécanisme de connexion entre le dispositif formel de la
découverte et les phénomènes reproductibles des environnements interne et
externe. En opérant
une synthèse de la découverte de l’énergie, il devient possible de prédire le
futur dans le reflet d’un segment d’événements futurs au sein d’un milieu où l’on
identifie des différences de température notables, ou bien dans un système
cristallin. Une élaboration détaillée des phénomènes de la réalité, combinée à
une synthèse simultanée de l’environnement de contrôle conduit aux systèmes de
synthèse ondulatoire. Décrire les processus de la réalité grâce au système de synthèse
ondulatoire consiste à considérer la réalité comme l’intersection périodique de
zones stationnaires et de zones dynamiques. A ces intersections, une synthèse
des ondes dynamiques et stationnaires a lieu. Le fait d’identifier la phase
dynamique dans le champ stationnaire permet d’atteindre un fonctionnement
infini du champ stationnaire. Dans les cristaux, un processus similaire permet,
en résolvant le problème inverse, d’obtenir à partir du milieu stationnaire (du
cristal) la composante dynamique de la synthèse ondulatoire (à savoir : la
phase temporelle). Voici la formule de la théorie de la synthèse ondulatoire
permettant de décrire la réalité :

où T : le temps, Y : l’onde de la phase dynamique de la réalité, S : la phase stationnaire de la réalité.
Dans certains cas, la synthèse ondulatoire de la réalité peut être vue comme une onde infinie qui traverse périodiquement les champs stationnaires, créant de nouvelles phases de réalité à chaque processus d’entrecroisement. En passant de la phase dynamique à la phase stationnaire, le fait de fixer ces composants les rend indépendants par rapport au temps, et de fait, éternels. En conséquence, l’objet créé dans un tel champ est éternel et pourra toujours être restauré [4]. Si on considère un séisme sous cet angle, les reflets situés à la surface des cristaux permettent d’identifier les critères pouvant restaurer l’environnement mesuré dans le temps. Il est ainsi possible de déterminer avec exactitude le moment où un tremblement de terre se produira. La théorie de la synthèse ondulatoire, lorsqu’elle s’applique à l’être humain, constitue la preuve de son immortalité. Selon cette théorie, l’immortalité peut être réalisée en convertissant le champ de reproduction de l’onde de la phase stationnaire de la réalité S en onde de la phase dynamique de la réalité Y. La production de gènes à partir des formes-pensées humaines atteste que cette conversion est avérée. Ainsi, dans les systèmes de reconnaissance optique et de contrôle des séismes, le système potentiellement éternel qu’est l’être humain interagit avec un système de cristaux dans le champ de production de l’onde stationnaire. Cette interaction permet de prédire le tremblement de terre et également de diminuer son intensité de façon harmonieuse. Un séisme de moindre intensité est enregistré. En sus, l’information de cet événement cesse d’être produite, ce qui augmente la durée de vie du dispositif. Dans ce cas, l’éternité potentielle de l’être humain augmente réellement les ressources de l’appareil. Ce qui est éternel fait naître ce qui est éternel. En général, tous les appareils et les mécanismes créés par l’homme doivent satisfaire à ces conditions. Selon le principe de rétroaction, ces appareils et mécanismes seront toujours créateurs pour l’être humain et ne pourront jamais lui porter atteinte, ni à son environnement, en aucune circonstance.
Pour élaborer les principes de fonctionnement de systèmes techniques à partir de cette technologie, il est nécessaire de convertir les lois de diffusion des signaux optiques. Dans certains cas, la synthèse ondulatoire de la réalité peut être vue comme une onde infinie qui traverse périodiquement les champs stationnaires, créant de nouvelles phases de réalité à chaque processus d’entrecroisement. En passant de la phase dynamique à la phase stationnaire, le fait de fixer ces composants les rend indépendants par rapport au temps, et de fait, éternels. En conséquence, l’objet créé dans un tel champ est éternel et pourra toujours être restauré [4]. Si on considère un séisme sous cet angle, les reflets situés à la surface des cristaux permettent d’identifier les critères pouvant restaurer l’environnement mesuré dans le temps. Il est ainsi possible de déterminer avec exactitude le moment où un tremblement de terre se produira. La théorie de la synthèse ondulatoire, lorsqu’elle s’applique à l’être humain, constitue la preuve de son immortalité. Selon cette théorie, l’immortalité peut être réalisée en convertissant le champ de reproduction de l’onde de la phase stationnaire de la réalité S en onde de la phase dynamique de la réalité Y. La production de gènes à partir des formes-pensées humaines atteste que cette conversion est avérée. Ainsi, dans les systèmes de reconnaissance optique et de contrôle des séismes, le système potentiellement éternel qu’est l’être humain interagit avec un système de cristaux dans le champ de production de l’onde stationnaire. Cette interaction permet de prédire le tremblement de terre et également de diminuer son intensité de façon harmonieuse. Un séisme de moindre intensité est enregistré. En sus, l’information de cet événement cesse d’être produite, ce qui augmente la durée de vie du dispositif. Dans ce cas, l’éternité potentielle de l’être humain augmente réellement les ressources de l’appareil. Ce qui est éternel fait naître ce qui est éternel. En général, tous les appareils et les mécanismes créés par l’homme doivent satisfaire à ces conditions. Selon le principe de rétroaction, ces appareils et mécanismes seront toujours créateurs pour l’être humain et ne pourront jamais lui porter atteinte, ni à son environnement, en aucune circonstance. Pour élaborer les principes de fonctionnement de systèmes techniques à partir de cette technologie, il est nécessaire de convertir les lois de diffusion des signaux optiques.
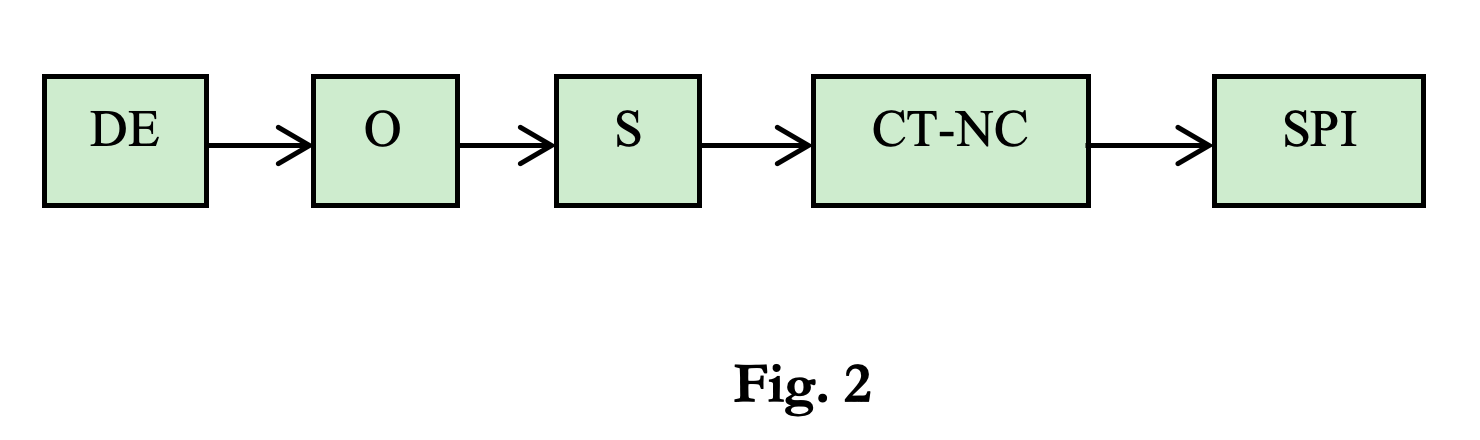
4. Étude des systèmes analytiques
des milieux optiques pour la prévention des séismes et des catastrophes
Des expériences sont effectuées sur les milieux optiques dans l’objectif de distinguer les différentes phases de l’impulsion optique, selon le principe consistant à minimiser la résistance du milieu le long de la trajectoire de l’impulsion. Plus précisément, il s’agit d’identifier le facteur mouvement ayant un coefficient d’absorption minimal. Dans un système de connexions universelles où tous les objets sont en interaction, y compris ceux qui appartiennent au futur et au passé, l’impulsion lumineuse est répartie en trois phases temporelles dans l’élément optique du présent. Selon la théorie de la synthèse ondulatoire, le présent peut être vu comme une onde dynamique, le passé comme un champ statique et le futur comme la phase synthétisée de la réalité, obtenue par la fixation du champ statique en une onde dynamique. La substance connue est créée par le biais du champ statique, tandis que la substance inconnue est créée dans la période initiale de synthèse de la réalité future. Dans les systèmes optiques, la partie événementielle correspondant au passé est définie comme un milieu optique aux caractéristiques fixes (un cristal, par exemple), pour le présent, comme une impulsion lumineuse, et, pour le futur, comme un champ synthétisé, issu de l’interaction entre l’impulsion lumineuse et le cristal.
Selon la distribution spécifiée, la formule de l’énergie du futur
Ψ = E∙W/U implique que les événements futurs, basés sur l’énergie future Ψ, sont définis par la valeur fixe de l’impulsion lumineuse émise E dans les conditions où U désigne l’espace du système optique, et W l’espace du système optique et les champs mesurés. Considérant que selon la formule de l'énergie passée E = Ep F, l'énergie du présent Ep est déterminée par la valeur actuelle (changeante) de l'impulsion lumineuse, nous pouvons déduire la fonction F sous forme d’une projection des champs mesurés sur le système analytique des milieux optiques. Le système analytique des milieux optiques est situé dans l'espace P qui contient le milieu optique aux propriétés fixes et le milieu optique contenant des zones changeantes d'intersection et de réflexion des impulsions lumineuses. Puisque W = Ψ ∙ W1(W)/EP selon la formule de la réalité générale, il est possible de déterminer les caractéristiques des phénomènes à partir d'un seul point : on déduit W1(W) pour l'espace P en tant que projection des zones de mesure sur P. En tenant compte de W dans la méthode de mesure, l'environnement optique redéfinit d'abord de manière créative et harmonieuse une réalité visant à prévenir ou diminuer l’intensité du séisme, puis détermine ensuite les paramètres du séisme. Dans le cas général, en utilisant l'expression de W, on peut transformer l'information d’une catastrophe éventuelle de sorte à l’éviter ou à réduire son impact. Selon la loi des connexions générales entre tous les phénomènes de la réalité, les résultats obtenus pour les systèmes optiques peuvent être transférés à tout support ayant des fonctions analogues. Il en découle que les phénomènes catastrophiques peuvent être mesurés et évités à partir de n'importe quel point de la réalité. Un dispositif doté d’un système optique est utilisé pour opérer un contrôle prévisionnel des phénomènes de la réalité visant à diminuer ou prévenir les événements catastrophiques, et les fonctions de ce dispositif sont déterminées par des critères d'impulsions lumineuses.
5. Dispositifs structurels et analytiques de prévention des séismes et des catastrophes
En
appliquant la structure des systèmes optiques obtenue dans notre étude, qui
permet de prévoir harmonieusement et de prévenir les catastrophes, il est
possible d’élaborer des dispositifs qui ne portent pas atteinte au temps ni
à
l’espace [5]. La catastrophe ne se produira donc pas car elle aura été évitée ou
réduite dans son impact. C’est ce principe d’harmonisation que doit régir la
fabrication de cet appareil comme de tous les autres objets, de sorte qu’ils ne
présentent aucun danger pour leur créateur comme pour son environnement.
Module cristal de prévision des
tremblements de terre et des catastrophes. Fonctions de création de substance
L’utilisation de
cristaux orientés permet de prévoir les séismes jusqu’à 7 jours à l’avance. Voici
le schéma de localisation des cristaux de roche (composition chimique : quartz,
système cristallin trigonal, dureté : 7.0, gravité spécifique : 2.65,
réfraction : 1.54 – 1.55, biréfringence : 0,009, dans leurs
projections sur des
plans de coordonnées :
sur le plan (O,x,y) où (O,x) représente l’axe
horizontal, (O,y) l’axe vertical

Le principe d'amplification de ces projections dues aux signaux réfléchis par les surfaces est inclus dans les conditions de division de l'impulsion lumineuse. Voici le principe à l’œuvre dans le dispositif étudié : quand la lumière se transforme dans un environnement optique spécifique, la forme d’un volume lumineux correspondant aux événements futurs peut être identifiée. Les cristaux sont disposés de manière à prévenir tout séisme ou catastrophe, en établissant un développement futur créateur à plus et à moins l’infini. Le rayonnement émis est normalisé, car selon la formule de la réalité générale, l’entrecroisement des composants lumineux et du niveau harmonieux des cristaux provoque la normalisation des processus de la réalité. Ce dispositif a été élaboré en appliquant le concept des propriétés créatives de tout dispositif technique. La lumière émise permet d’obtenir des informations sur le moment et l’intensité d'un séisme 7 jours à l’avance. Les surfaces des cubes de cristal de roche doivent être aussi plates que possible, avec une précision de traitement allant jusqu'au micromètre. L'absorption en surface d'une onde monochromatique d'une longueur de 4,3 • 10-7 par impulsion nanoseconde devrait être de 0,5 avec un coefficient de réflexion de la carte géographique égal à 0,62. Les propriétés de la surface doivent être modifiées dans l'intervalle correspondant à la durée de vie du dispositif, qui fait neuf mois. Elle peut être augmentée en y ajoutant une lentille optique externe. Après les neuf premiers mois d’exploitation du dispositif, il est nécessaire de calculer le décalage des lentilles tous les 5 mois. Après trois premières périodes de cinq mois, on compte trois périodes de quatre mois et ainsi de suite, jusqu'à des périodes de dix jours. Ensuite, il faut modifier la forme de la lentille. On peut relever les paramètres de sortie en mesurant les caractéristiques de la lumière du côté de la sphère opposé à la carte ou au terrain. Si les caractéristiques de la lumière changent de plus de 25% par milliseconde dans la zone mesurée, on identifie le profil d'un séisme, d'intensité 3 points à son épicentre, qui aura lieu en 14 jours à partir du moment de la mesure. L'épicentre du tremblement de terre est déterminé en scannant des segments de la zone à mesurer. Dans le cas étudié, les caractéristiques de la lumière au sein de l'épicentre changent de 32% par milliseconde.
Concernant les installations industrielles, on mesure le schéma de fonctionnement de l'ensemble de la production. En cas de changement des caractéristiques de la lumière de plus de 14 % par milliseconde sur le site mesuré, les écarts à la norme doivent être signalés dans un délai de 14 jours à compter du moment de l'enregistrement. Pour identifier avec précision le processus pouvant présenter des déviations par rapport à la norme, il faut zoomer sur la section localisée du schéma et la mesure suivante. Dans l'élément du système à l'origine des anomalies, on observe une modification des caractéristiques de la lumière de 32 % par milliseconde.
En général, tout événement de la réalité peut être schématisé et mesuré par ce dispositif, dans l’objectif d’opérer un contrôle prévisionnel des événements. Le contrôle des événements peut parfois impliquer la création d’une substance aux caractéristiques spécifiques (par exemple, la restauration urgente du microprocesseur d’un avion en chute libre). On peut donc orienter spécifiquement le dispositif sur ce processus, en plaçant le schéma de la substance (dans cet exemple, le circuit du microprocesseur) au-dessus du troisième cristal du module. En utilisant ce mécanisme pour créer la substance nécessaire et en appliquant les principes disponibles dans le module cristal, il est possible de créer des productions fiables et sans danger pour l’environnement.Les systèmes optiques dans le contrôle des microprocessus
Pour certains processus, une méthode est utilisée pour calculer les caractéristiques des appareils et des surfaces de mesure. Pour d'autres processus, une autre méthode de calcul doit être élaborée. Dans certains cas, lorsque la schématisation du phénomène ne reflète pas complètement les paramètres nécessaires à la mesure (par exemple, pour les microprocessus à vitesse élevée ou certaines catastrophes à caractère global), on applique des possibilités irrationnelles de définition des données constructives du dispositif. Considérant que tout phénomène de la réalité, y compris inconnu, peut être décrit de manière schématique, ce dispositif nous permet d'identifier et de prévenir des processus catastrophiques pouvant survenir dans des zones inconnues de la réalité.
Selon la théorie de la synthèse ondulatoire, le contrôle des microprocessus a lieu dans le champ du système optique où s’effectue la synthèse. En microélectronique, les définitions fondamentales des systèmes optiques s’appliquent sur une base à multiples composants. Chacun de ces composants peut être défini grâce à plusieurs paramètres, qui sont également interdépendants. Selon les lois de la mécanique quantique à l’œuvre dans le volume élémentaire dτp et l’impulsion, l’espace P des états quantiques contient :
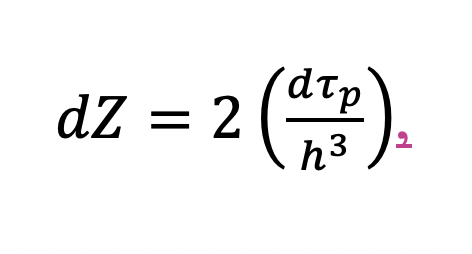
En supposant que les surfaces isoénergétiques de l'espace P sont représentées par des sphères, il est possible, sur la base de la théorie de la synthèse ondulatoire, de contrôler le nombre d'états quantiques N(E) en transformant la forme d'information correspondant à la masse effective d’un électron proche du fond du champ conducteur mn, en une impulsion du système optique qui le contrôle. À cette fin, les paramètres de transformation nécessaires sont placés sur le quatrième cristal. Cette technologie peut être utilisée pour orienter les méthodes de fabrication de dispositifs moléculaires vers une sécurité environnementale totale.
Nous nous sommes basés sur les définitions fondamentales des systèmes optiques pour obtenir des données permettant d’élaborer un dispositif de prévision et de prévention des catastrophes. La fonction de ce dispositif, basé sur l'analyse des flux lumineux, est de diminuer ou d’empêcher toute catastrophe de façon harmonieuse. La correction effectuée par ce dispositif permet de diminuer au maximum les paramètres de la catastrophe et de déterminer les caractéristiques de sa manifestation. Selon la loi des connexions universelles, ces structures instrumentales et analytiques ne présentent aucun danger pour les personnes et l'environnement, car elles sont basées sur les caractéristiques inoffensives de la lumière. L’utilisation du composant de contrôle du système optique permet de créer la réalité voulue. Les définitions fondamentales des systèmes optiques sont formulées ainsi :
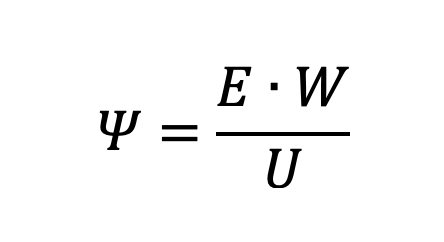


Le champ d’application de cette définition de la réalité générale dans les systèmes optiques conducteurs permet d’identifier une impulsion transformant n’importe quel milieu, afin de contrôler la réalité. Plus généralement, cette découverte permet de déterminer tous les phénomènes de la réalité.
Selon la première loi, les systèmes optiques à base de cristaux reproduisent le reflet d'événements futurs, ayant traversé d’une picoseconde l’intervalle du passé.
La seconde loi est celle du mouvement du signal optique, orienté à la fois vers les systèmes de fixation et vers un environnement aux propriétés indéfinies. Dans ce contexte, il est possible de distinguer la constante informationnelle déterminant le contrôle des environnements à structure indéterminée.
Selon la troisième loi, en reconnaissant le champ de projection du futur sur le présent, sur la base d’une impulsion variée en fonction des différents matériaux les différents milieux, la structure d’un dispositif harmonisant tous les systèmes peut être établie.
Selon la quatrième loi, le système défini par un signal optique est toujours défini pour des processus infinis. Il découle de cette quatrième loi que tous les processus de la réalité peuvent être décrit dans chacun de ses champs. La théorie de la synthèse ondulatoire en résulte. Voici la formule de la théorie de la synthèse ondulatoire permettant de décrire la réalité :
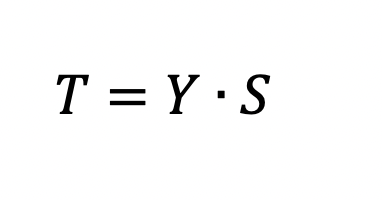
Des expériences sont effectuées sur les milieux optiques dans l’objectif de distinguer les différentes phases de l’impulsion optique, selon le principe consistant à minimiser la résistance du milieu le long de la trajectoire de l’impulsion.
En appliquant la structure des systèmes optiques obtenue dans notre étude, qui permet de prévoir harmonieusement et de prévenir les catastrophes, il est possible d’élaborer des dispositifs qui ne portent pas atteinte au temps ni à l’espace [5]. La catastrophe ne se produira donc pas car elle aura été évitée ou réduite dans son impact. C’est ce principe d’harmonisation que doit régir la fabrication de cet appareil comme de tous les autres objets, de sorte qu’ils ne présentent aucun danger pour leur créateur comme pour son environnement. Le module cristal de prévision des tremblements de terre a été élaboré suivant ce principe.
En général, tout événement de la réalité peut être schématisé et mesuré par ce dispositif, dans l’objectif d’opérer un contrôle prévisionnel des événements. Pour un certain nombre de processus de la réalité (par exemple, pour les microprocessus à vitesse élevée ou certaines catastrophes à caractère global), les paramètres du dispositif sont calculés en appliquant des possibilités sensorielles qui tiennent compte de la compréhension de la loi des connexions universelles. La prise en compte d’une approche irrationnelle pour calculer les paramètres du dispositif confère à ce dispositif une fonction permettant d’analyser et de déterminer des propriétés inconnues de la réalité.
Annexe
Méthodes
de calcul quantitatif du module cristallin de prévision des tremblements de
terre et des catastrophes
Introduction
Pour
obtenir un calcul quantitatif, il est nécessaire de considérer l'ensemble du
processus de fonctionnement du dispositif et de déterminer les conditions aux
limites et les conditions initiales pour tous les cycles intermédiaires du
processus. En étudiant le processus de passage de la lumière à travers le
dispositif, et en mesurant ses caractéristiques de sortie, on constate que la
température mesurée au niveau du cristal nous renseigne sur l’information de
sortie. En se basant sur la théorie de la synthèse ondulatoire, on constate qu’il
est possible, dans les calculs, de compléter le champ de l’onde statique de la
réalité par celui de l’onde dynamique. Toutes les caractéristiques nécessaires
à la mesure peuvent donc être identifiées dans le champ de production de la
réalité. Dans ce cas précis, en désignant le rayonnement issu du champ de
mesure par le champ de l’onde statique de la réalité S, le rayonnement
laser situé près de l’objet mesuré et fixé au dispositif peut être considéré
comme l’onde dynamique de la réalité Y. Il est alors possible de déterminer
le moment T où se produira le séisme en fonction du barème établi,
en tenant compte de l'influence du rayonnement laser sur le barème de mesure
des paramètres de sortie de l'appareil. Selon la théorie de la synthèse
ondulatoire, le rayonnement laser amplifie les paramètres informationnels du
rayonnement lumineux perçu.
L’impact du laser sur
le matériau du dispositif doit être dirigé en fonction des caractéristiques du
rayonnement de l'objet mesuré.
Ce processus d’impact doit être étudié, afin de définir la réaction des matériaux utilisés dans la construction de l’appareil et d’émettre des recommandations pour la conception future. La difficulté de la recherche est conditionnée par l’interdépendance entre les processus en cours, les caractéristiques thermophysiques du matériau, et les caractéristiques énergétiques du rayonnement laser. Pour chaque cas spécifique d’interaction entre le rayon laser et le matériau, un modèle mathématique bien défini doit être établi afin de décrire le processus physique réel, en se basant sur des hypothèses mettant en adéquation ce modèle et les processus physiques réels. Les articles, journaux scientifiques et monographies présentent des solutions à des problèmes particuliers, comportant cependant un certain nombre de limitations caractéristiques à leur modèle d'interaction. C'est pourquoi la nécessité de modéliser mathématiquement cette interaction avec les matériaux donnés est apparue. Selon moi, l’élaboration d'un modèle mathématique décrivant ce processus physique avec suffisamment de précision ne peut se passer d’une confirmation expérimentale. Sur cette base, j'ai utilisé une méthode computationnelle et expérimentale pour résoudre ce problème, consistant à le modéliser numériquement en convertissant chaque objet informationnel en une forme géométrique.
Le dispositif se présente donc sous la forme d’un module cristallin, dont le premier cristal est orienté vers l’objet à mesurer, tandis qu’un thermocouple est fixé à la paroi du dernier cristal. Des informations sont obtenues par la mesure des caractéristiques de sortie effectuée grâce à un thermocouple. L’avantage de cette source d’information est qu’elle est très résistante aux interférences. L’application de la théorie de la synthèse ondulatoire par l'utilisation du rayonnement résout également le problème de la stabilité du signal émanant de l'objet mesuré. Comme le rayonnement issu de l’objet mesuré constitue la tâche particulière du processus du rayonnement laser, dans cette option où les caractéristiques sont mesurées avec le thermocouple, l’essentiel est ici de calculer le processus du rayonnement laser.
1. Interaction
du rayonnement laser continu et des matériaux
1.1. Propagation
de la chaleur dans une couche de substance homogène
L'état
thermique du matériau irradié et le caractère des processus physiques sont
déterminés par les caractéristiques énergétiques du rayonnement laser : la
densité de flux et le temps d'exposition au rayonnement laser, la distribution
spatiale et les paramètres géométriques de l'intensité du rayon, ainsi que les caractéristiques
thermophysiques du matériau irradié.
L'énergie
du rayonnement laser E concentré sur la surface du matériau irradié se
répartit comme suit :
E = Eref + Eabs + Etrav
où Eref :
énergie réfléchie de manière diffuse par la surface irradiée, Eabs :
énergie du rayonnement laser absorbée par le matériau, Etrav : énergie
du rayonnement laser qui traverse le matériau (pour les matériaux
transparents).
Seule la
partie absorbée de l'énergie a été prise en compte.
Dans
cette étude, on utilise la théorie classique de la conduction thermique pour
calculer la façon dont les matériaux se réchauffent.
Cette
approche se base sur le fait que l'énergie lumineuse se transforme
instantanément en chaleur dans le point d’absorption de la lumière. L'énergie
est distribuée si rapidement qu'un équilibre local est assuré pendant toute la
durée de l'exposition. On peut donc utiliser la notion de température et les
équations habituelles pour décrire le flux thermique.
Dans les
cas intéressants sur le plan pratique, le problème peut être vu comme
unidimensionnel. C’est possible dans le cas où les dimensions transversales du
rayon laser sont importantes par rapport à la profondeur à laquelle la chaleur
se propage pendant la période d’exposition, et lorsque la chaleur se diffusant dans
d’autres directions peut être calculée grâce au modèle de propagation de la chaleur
dans une couche hétérogène de substance, décrit ci-dessous. On peut utiliser le
principe d'intégration des températures distribuées pour spécifier les
caractéristiques de la distribution spatiale du rayonnement. Toutefois, cela
n’est pas indispensable car la théorie de la synthèse ondulatoire permet d'obtenir
tous les détails nécessaires à tout moment du processus, selon la méthode des
phases statique et dynamique de la réalité exposée dans l'introduction et basée
sur les découvertes fondamentales des systèmes optiques. L'intensité du
rayonnement laser dans le faisceau est considérée comme cylindrique et uniforme.
Le coefficient d'absorption du rayonnement laser A dépend de la température.
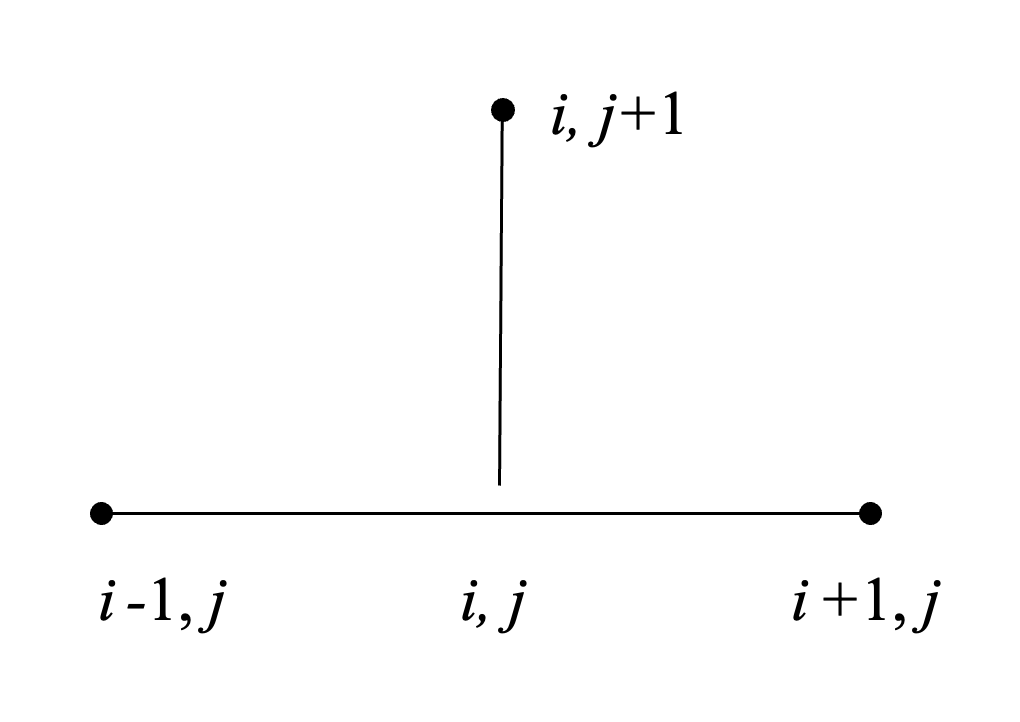
L'équation différentielle décrivant la propagation de la chaleur dans une
couche homogène de substance se présente ainsi :
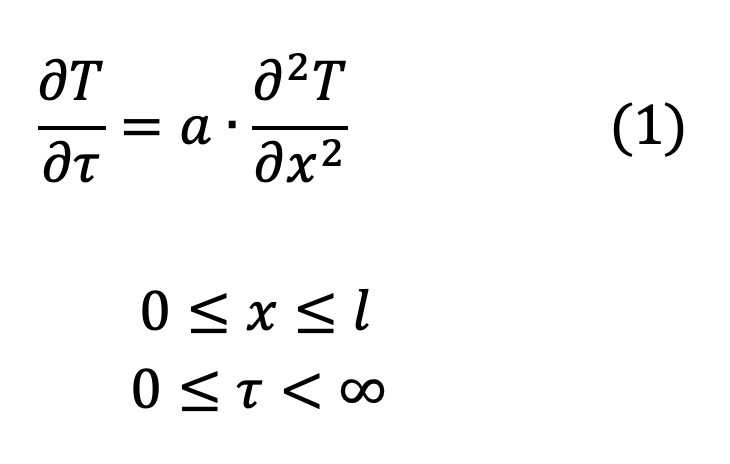
Condition initiale :

Condition aux limites sur la surface irradiée :